Dictionaries and dataframes#
Needing a better way of ordering dictionaries was one of the original inspirations for Sciris back in 2014. In those dark days of Python <=3.6, dictionaries were unordered, which meant that dict.keys() could give you anything. (And you still can’t do dict.keys()[0], much less dict[0]). This tutorial describes Sciris’ ordered dict, the odict, its close cousin the objdict, and its pandas-powered pseudorelative, the dataframe.
Click here to open an interactive version of this notebook.
The odict#
In basically every situation except one, an odict can be used like a dict. (Since this is a tutorial, see if you can intuit what that one situation is!) For example, creating an odictworks just like creating a regular dict:
[1]:
import sciris as sc
od = sc.odict(a=['some', 'strings'], b=[1,2,3])
print(od)
#0: 'a': ['some', 'strings']
#1: 'b': [1, 2, 3]
Okay, it doesn’t exactly look like a dict, but it is one:
[2]:
print(f'Keys: {od.keys()}')
print(f'Values: {od.values()}')
print(f'Items: {od.items()}')
Keys: ['a', 'b']
Values: [['some', 'strings'], [1, 2, 3]]
Items: [('a', ['some', 'strings']), ('b', [1, 2, 3])]
Looks pretty much the same as a regular dict, except that od.keys() returns a regular list (so, yes, you can do od.keys()[0]). But, you can do things you can’t do with a regular dict, such as:
[3]:
for i,k,v in od.enumitems():
print(f'Item {i} is called {k} and has value {v}')
Item 0 is called a and has value ['some', 'strings']
Item 1 is called b and has value [1, 2, 3]
We can, as you probably guessed, also retrieve items by index as well:
[4]:
print(od['a'])
print(od[0])
['some', 'strings']
['some', 'strings']
Remember the question about the situation where you wouldn’t use an odict? The answer is if your dict has integer keys, then although you still could use an odict, it’s probably best to use a regular dict. But even float keys are fine to use (if somewhat strange).
You might’ve noticed that the odict has more verbose output than a regular dict. This is because its primary purpose is as a high-level container for storing large(ish) objects.
For example, let’s say we want to store a number of named simulation results. Look at how we’re able to leverage the odict in the loop that creates the plots
[5]:
import numpy as np
import pylab as pl
class Sim:
def __init__(self, n=20, n_factors=6):
self.results = sc.odict()
self.n = n
self.n_factors = n_factors
def run(self):
for i in range(self.n_factors):
label = f'y = N^{i+1}'
result = np.random.randn(self.n)**(i+1)
self.results[label] = result
def plot(self):
with sc.options.context(jupyter=True): # Jupyter-optimized plotting
pl.figure()
rows,cols = sc.getrowscols(len(self.results))
for i,label,result in self.results.enumitems(): # odict magic!
pl.subplot(rows, cols, i+1)
pl.scatter(np.arange(self.n), result, c=result, cmap='parula')
pl.title(label)
sc.figlayout() # Trim whitespace from the figure
sim = Sim()
sim.run()
sim.plot()
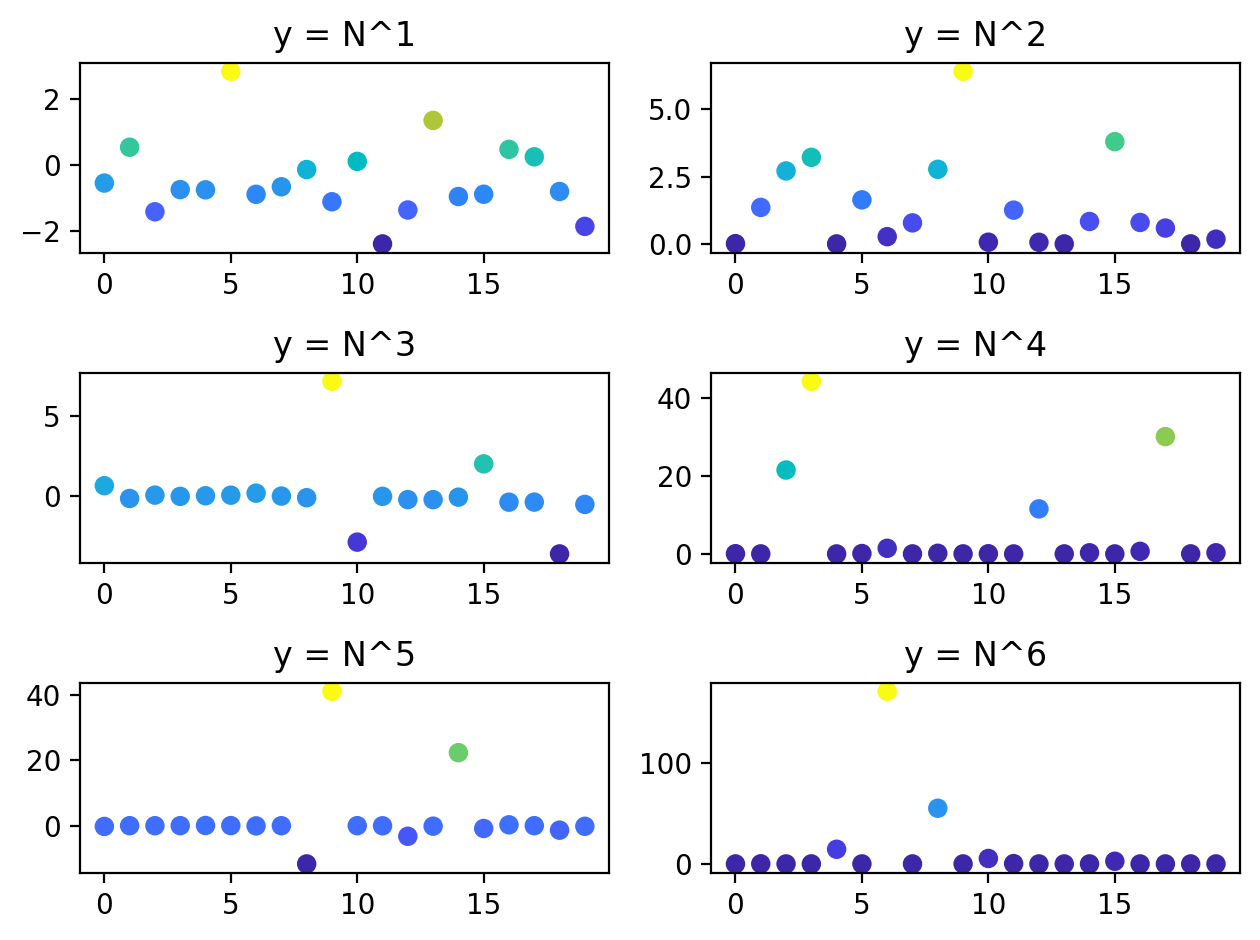
We can quickly access these results for exploratory data analysis without having to remember and type the labels explicitly:
[6]:
print('Sim results are')
print(sim.results)
print('The first set of results is')
print(sim.results[0])
print('The first set of results has median')
sc.printmedian(sim.results[0])
Sim results are
#0: 'y = N^1':
array([-0.54016972, 0.54049209, -1.40646494, -0.73719452, -0.74496715,
2.83032182, -0.87933836, -0.65211419, -0.13288216, -1.10391221,
0.11377512, -2.37603465, -1.35245841, 1.34875231, -0.94662911,
-0.87763284, 0.47554452, 0.25084 , -0.79472331, -1.84704125])
#1: 'y = N^2':
array([1.03262706e-02, 1.35456400e+00, 2.70620145e+00, 3.21129521e+00,
6.03875928e-04, 1.63405220e+00, 2.69367871e-01, 7.80657402e-01,
2.76728446e+00, 6.40165649e+00, 6.43326833e-02, 1.25308353e+00,
6.06377072e-02, 6.91062330e-06, 8.32721320e-01, 3.79333343e+00,
7.95878583e-01, 5.88378319e-01, 2.31384103e-03, 1.76826542e-01])
#2: 'y = N^3':
array([ 6.64836788e-01, -1.35990256e-01, 7.48025386e-02, -4.33966724e-03,
3.27891266e-02, 7.03836176e-02, 1.96451012e-01, 1.46180983e-02,
-8.81772149e-02, 7.20469112e+00, -2.87054190e+00, -2.11123473e-03,
-2.06484315e-01, -2.09488878e-01, -5.44535601e-02, 2.03248758e+00,
-3.66714552e-01, -3.63381686e-01, -3.60970122e+00, -5.08318972e-01])
#3: 'y = N^4':
array([5.74118981e-02, 1.05249326e-02, 2.15752454e+01, 4.43863464e+01,
1.12007956e-04, 1.00339723e-01, 1.45197533e+00, 1.14267287e-02,
1.63523380e-01, 1.42164766e-02, 4.75173627e-02, 9.86919645e-08,
1.15851385e+01, 9.84085292e-03, 2.91701735e-01, 7.35441544e-04,
6.61696371e-01, 3.01576269e+01, 1.68033509e-02, 2.98005002e-01])
#4: 'y = N^5':
array([-2.28533162e-01, 1.13613751e-05, -1.19251281e-02, 4.81322573e-03,
6.33689600e-02, 2.74856360e-02, -6.41970894e-02, -9.88575519e-03,
-1.17046666e+01, 4.11312024e+01, 4.52099821e-05, -3.29798655e-02,
-3.24457869e+00, -1.45264592e-01, 2.23440640e+01, -8.54890805e-01,
2.61914419e-01, 1.08767892e-03, -1.37680945e+00, -1.83465829e-01])
#5: 'y = N^6':
array([6.75146146e-05, 1.25063025e-01, 1.26266318e-04, 2.84635575e-02,
1.46171972e+01, 2.00562911e-02, 1.71858281e+02, 4.52896845e-03,
5.54399758e+01, 9.15985733e-10, 5.43303074e+00, 2.98186547e-01,
7.96640075e-04, 2.52947905e-03, 2.21160411e-02, 2.67231079e+00,
5.14794085e-08, 6.77497582e-05, 1.13131751e-04, 6.26424531e-05])
The first set of results is
[-0.54016972 0.54049209 -1.40646494 -0.73719452 -0.74496715 2.83032182
-0.87933836 -0.65211419 -0.13288216 -1.10391221 0.11377512 -2.37603465
-1.35245841 1.34875231 -0.94662911 -0.87763284 0.47554452 0.25084
-0.79472331 -1.84704125]
The first set of results has median
-0.741 (95% CI: -2.125, 2.127)
This is a have-your-cake-and-eat-it-too situation: the first set of results is correctly labeled (sim.results['y = N^1']), but you can easily access it without having to type all that (sim.results[0]).
The objdict#
When you’re just writing throwaway analysis code, it can be a pain to type mydict['key1']['key2'] over and over. (Right-pinky overuse is a real medical issue.) Wouldn’t it be nice if you could just type mydict.key1.key2, but otherwise have everything work exactly like a dict? This is where the objdict comes in: it’s identical to an odict (and hence like a regular dict), except you can use “object syntax” (a.b)
instead of “dict syntax” (a['b']). This is especially handy for using f-strings, since you don’t have to worry about nested quotes:
[7]:
ob = sc.objdict(key1=['some', 'strings'], key2=[1,2,3])
print(f'Checking {ob[0] = }')
print(f'Checking {ob.key1 = }')
print(f'Checking {ob["key1"] = }') # We need to use double-quotes inside since single quotes are taken!
Checking ob[0] = ['some', 'strings']
Checking ob.key1 = ['some', 'strings']
Checking ob["key1"] = ['some', 'strings']
In most cases, you probably want to use objdicts rather than odicts just to have the extra flexibility. Why would you ever use an odict over an objdict? Mostly just because there’s small but nonzero overhead in doing the extra attribute checking: odict is faster (faster than even collections.OrderedDict, though slower than a plain dict). The differences are tiny (literally nanoseconds) so won’t matter unless you’re doing millions of operations. But if you’re
reading this, chances are high that you do sometimes need to do millions of dict operations.
Dataframes#
The Sciris sc.dataframe() works exactly like pandas pd.DataFrame(), with a couple extra features, mostly to do with creation, indexing, and manipulation.
Dataframe creation#
Any valid pandas dataframe initialization works exactly the same in Sciris. However, Sciris is a bit more flexible about how you can create the dataframe, again optimized for letting you make them quickly with minimal code. For example:
[8]:
import pandas as pd
x = ['a','b','c']
y = [1, 2, 3]
z = [1, 0, 1]
df = pd.DataFrame(dict(x=x, y=y, z=z)) # Pandas
df = sc.dataframe(x=x, y=y, z=z) # Sciris
It’s not a huge difference, but the Sciris one is shorter. Sciris also makes it easier to define types on dataframe creation:
[9]:
df = sc.dataframe(x=x, y=y, z=z, dtypes=[str, float, bool])
print(df)
x y z
0 a 1.0 True
1 b 2.0 False
2 c 3.0 True
You can also define data types along with the columns:
[10]:
columns = dict(x=str, y=float, z=bool)
data = [
['a', 1, 1],
['b', 2, 0],
['c', 3, 1],
]
df = sc.dataframe(columns=columns, data=data)
df.disp()
x y z
0 a 1.0 True
1 b 2.0 False
2 c 3.0 True
The df.disp() command will do its best to show the full dataframe. By default, Sciris dataframes (just like pandas) are shown in abbreviated form:
[11]:
df = sc.dataframe(data=np.random.rand(70,10))
print(df)
0 1 2 3 4 5 6 \
0 0.068829 0.241926 0.682636 0.881461 0.169705 0.692593 0.380404
1 0.248104 0.780141 0.718935 0.791855 0.748851 0.487138 0.074483
2 0.518904 0.683791 0.287663 0.707347 0.853853 0.668351 0.132939
3 0.984054 0.259648 0.255607 0.078166 0.617954 0.855227 0.754584
4 0.341654 0.081161 0.150890 0.697708 0.029461 0.793399 0.191758
.. ... ... ... ... ... ... ...
65 0.287400 0.530047 0.868400 0.777354 0.465318 0.899153 0.084952
66 0.121803 0.073402 0.869759 0.009655 0.186355 0.722959 0.497785
67 0.972743 0.533272 0.432389 0.534526 0.823315 0.947444 0.510858
68 0.719464 0.754241 0.800823 0.099966 0.246951 0.783649 0.433527
69 0.856336 0.800341 0.856466 0.857087 0.470238 0.238030 0.153689
7 8 9
0 0.243757 0.304405 0.545881
1 0.505455 0.247395 0.513261
2 0.292416 0.051455 0.710364
3 0.688046 0.255058 0.567092
4 0.867201 0.392203 0.477744
.. ... ... ...
65 0.690331 0.074770 0.647247
66 0.687649 0.213036 0.625880
67 0.912658 0.731800 0.934272
68 0.219143 0.000124 0.061581
69 0.059932 0.916551 0.338985
[70 rows x 10 columns]
But sometimes you just want to see the whole thing. The official way to do it in pandas is with pd.options_context, but this is a lot of effort if you’re just poking around in a script or terminal (which, if you’re printing a dataframe, you probably are). By default, df.disp() shows the whole damn thing:
[12]:
df.disp()
0 1 2 3 4 5 6 7 8 9
0 0.0688 0.2419 0.6826 0.8815 0.1697 0.6926 0.3804 0.2438 0.3044 0.5459
1 0.2481 0.7801 0.7189 0.7919 0.7489 0.4871 0.0745 0.5055 0.2474 0.5133
2 0.5189 0.6838 0.2877 0.7073 0.8539 0.6684 0.1329 0.2924 0.0515 0.7104
3 0.9841 0.2596 0.2556 0.0782 0.6180 0.8552 0.7546 0.6880 0.2551 0.5671
4 0.3417 0.0812 0.1509 0.6977 0.0295 0.7934 0.1918 0.8672 0.3922 0.4777
5 0.3446 0.7548 0.5690 0.3887 0.8617 0.5396 0.8991 0.6139 0.7869 0.8014
6 0.9610 0.7713 0.0052 0.3632 0.5823 0.4254 0.0710 0.1985 0.9791 0.8879
7 0.7300 0.2108 0.2462 0.9431 0.4787 0.0296 0.2279 0.6451 0.6524 0.0599
8 0.5914 0.8808 0.1240 0.9635 0.7500 0.1953 0.5162 0.6061 0.7892 0.5430
9 0.8725 0.0475 0.4655 0.1811 0.6285 0.1263 0.4667 0.7709 0.7521 0.0140
10 0.2478 0.2674 0.0546 0.3918 0.9033 0.5426 0.8303 0.0789 0.1589 0.1681
11 0.6500 0.3115 0.6682 0.2405 0.7116 0.2016 0.6633 0.5882 0.4821 0.6737
12 0.1827 0.1417 0.7272 0.8353 0.1033 0.2786 0.5160 0.5508 0.0655 0.3077
13 0.2035 0.9075 0.5474 0.7481 0.4970 0.9446 0.3011 0.3672 0.8236 0.3308
14 0.1145 0.8153 0.7400 0.9226 0.3878 0.0397 0.9604 0.4536 0.6970 0.1307
15 0.9345 0.2955 0.2890 0.6552 0.5069 0.9101 0.8020 0.1375 0.5055 0.1282
16 0.2508 0.6016 0.8613 0.8011 0.0106 0.1232 0.2061 0.9371 0.6674 0.3908
17 0.6847 0.8129 0.2201 0.2736 0.8626 0.7855 0.5447 0.2472 0.2908 0.9982
18 0.2125 0.1723 0.2516 0.8522 0.9286 0.6729 0.7500 0.0694 0.4912 0.7800
19 0.1246 0.1820 0.2288 0.2676 0.5196 0.1966 0.8938 0.9926 0.4833 0.8006
20 0.2539 0.8957 0.1875 0.4169 0.5024 0.7749 0.8566 0.3410 0.1210 0.4529
21 0.9511 0.2473 0.8047 0.9847 0.6583 0.4827 0.5275 0.7395 0.1190 0.1450
22 0.3049 0.2177 0.7142 0.4809 0.9941 0.2988 0.6830 0.1933 0.2663 0.0522
23 0.5462 0.4258 0.8021 0.9475 0.9271 0.9405 0.3673 0.9466 0.9162 0.0894
24 0.1176 0.5949 0.9471 0.1546 0.9394 0.1604 0.8790 0.8536 0.6946 0.1694
25 0.6818 0.9369 0.4188 0.4812 0.2541 0.7793 0.9329 0.9316 0.8520 0.2918
26 0.4045 0.6754 0.7968 0.3600 0.6089 0.0587 0.0246 0.9297 0.3781 0.7141
27 0.1728 0.4030 0.5822 0.8054 0.2649 0.9627 0.1023 0.7473 0.3939 0.9048
28 0.3638 0.3582 0.7914 0.6361 0.3271 0.5739 0.2361 0.2690 0.5097 0.1470
29 0.0416 0.5909 0.3645 0.1136 0.7435 0.6902 0.1362 0.5343 0.3330 0.3016
30 0.4766 0.8512 0.9706 0.8876 0.2547 0.0289 0.0397 0.9713 0.4744 0.3383
31 0.1613 0.4683 0.5405 0.6570 0.2270 0.2051 0.4478 0.1183 0.4998 0.9388
32 0.9060 0.7229 0.0421 0.3559 0.3631 0.1381 0.3900 0.7697 0.0610 0.7826
33 0.7877 0.4545 0.3434 0.3541 0.1322 0.2254 0.6850 0.2553 0.1322 0.6040
34 0.1953 0.5863 0.3579 0.9078 0.1122 0.3918 0.2104 0.4307 0.4514 0.1508
35 0.4782 0.8472 0.0019 0.6280 0.4576 0.6448 0.6920 0.2695 0.6703 0.3597
36 0.4026 0.8658 0.2599 0.9754 0.4449 0.9216 0.9235 0.7847 0.2513 0.8303
37 0.3907 0.4061 0.4413 0.6886 0.0100 0.4628 0.9032 0.7428 0.5912 0.8380
38 0.0288 0.2822 0.2435 0.7993 0.0838 0.4658 0.8373 0.9531 0.8186 0.2171
39 0.5674 0.5217 0.0611 0.5889 0.3574 0.4113 0.2085 0.6188 0.4565 0.8834
40 0.8627 0.5539 0.0616 0.3374 0.8617 0.0440 0.9283 0.6527 0.1154 0.3695
41 0.6180 0.8868 0.0093 0.8453 0.7134 0.8029 0.8075 0.9344 0.3582 0.0642
42 0.3415 0.4411 0.0952 0.2280 0.9467 0.6402 0.7704 0.2491 0.1224 0.8246
43 0.0038 0.8099 0.2127 0.9253 0.6545 0.2960 0.8862 0.6199 0.4815 0.8786
44 0.4773 0.0309 0.8233 0.1599 0.4644 0.6569 0.3903 0.8771 0.5275 0.2151
45 0.5052 0.4759 0.8976 0.2452 0.8920 0.9158 0.6642 0.4116 0.4561 0.1146
46 0.7042 0.3309 0.3871 0.5703 0.5064 0.1761 0.1945 0.1771 0.1294 0.1412
47 0.7374 0.7482 0.5953 0.7103 0.7889 0.5241 0.0049 0.3054 0.9225 0.8611
48 0.3578 0.4525 0.0622 0.2354 0.1427 0.6407 0.4946 0.7127 0.8434 0.7161
49 0.2164 0.5784 0.2846 0.0209 0.1487 0.8037 0.8088 0.9023 0.1076 0.9531
50 0.9659 0.9114 0.3567 0.6589 0.7454 0.3466 0.6390 0.9471 0.9515 0.8990
51 0.1144 0.9875 0.2862 0.3171 0.2284 0.5542 0.6006 0.0338 0.4961 0.8604
52 0.6379 0.7656 0.8104 0.8420 0.5057 0.0326 0.0436 0.2195 0.7790 0.3235
53 0.0293 0.3355 0.4341 0.1196 0.2086 0.1097 0.9650 0.0960 0.0220 0.8998
54 0.4761 0.6993 0.2631 0.9201 0.6151 0.3940 0.1397 0.7004 0.3467 0.1893
55 0.0789 0.0482 0.6698 0.4154 0.7079 0.8237 0.2328 0.8455 0.5686 0.4393
56 0.2845 0.3639 0.7660 0.8642 0.4647 0.2381 0.6505 0.9743 0.3807 0.0584
57 0.0188 0.4740 0.3770 0.2315 0.8721 0.6522 0.0615 0.5997 0.6090 0.3211
58 0.9146 0.1521 0.0843 0.7329 0.1864 0.6070 0.7472 0.2426 0.8733 0.9534
59 0.7767 0.6267 0.5570 0.4073 0.7933 0.1704 0.9963 0.6588 0.5234 0.1957
60 0.6101 0.3103 0.7323 0.3271 0.6262 0.3373 0.1567 0.2305 0.7151 0.2405
61 0.5336 0.3304 0.5324 0.9642 0.2002 0.5748 0.9263 0.8270 0.5639 0.8276
62 0.4606 0.3458 0.9793 0.6902 0.7007 0.4193 0.7739 0.6563 0.0632 0.5321
63 0.7706 0.1433 0.5348 0.3519 0.4583 0.2515 0.3233 0.9482 0.7797 0.4473
64 0.1789 0.3919 0.5088 0.6881 0.7114 0.1602 0.6840 0.1926 0.0170 0.8583
65 0.2874 0.5300 0.8684 0.7774 0.4653 0.8992 0.0850 0.6903 0.0748 0.6472
66 0.1218 0.0734 0.8698 0.0097 0.1864 0.7230 0.4978 0.6876 0.2130 0.6259
67 0.9727 0.5333 0.4324 0.5345 0.8233 0.9474 0.5109 0.9127 0.7318 0.9343
68 0.7195 0.7542 0.8008 0.1000 0.2470 0.7836 0.4335 0.2191 0.0001 0.0616
69 0.8563 0.8003 0.8565 0.8571 0.4702 0.2380 0.1537 0.0599 0.9166 0.3390
You can also pass other options if you want to customize it further:
[13]:
df.disp(precision=1, ncols=5, nrows=10, colheader_justify='left')
0 1 ... 8 9
0 6.9e-02 2.4e-01 ... 3.0e-01 5.5e-01
1 2.5e-01 7.8e-01 ... 2.5e-01 5.1e-01
2 5.2e-01 6.8e-01 ... 5.1e-02 7.1e-01
3 9.8e-01 2.6e-01 ... 2.6e-01 5.7e-01
4 3.4e-01 8.1e-02 ... 3.9e-01 4.8e-01
.. ... ... ... ... ...
65 2.9e-01 5.3e-01 ... 7.5e-02 6.5e-01
66 1.2e-01 7.3e-02 ... 2.1e-01 6.3e-01
67 9.7e-01 5.3e-01 ... 7.3e-01 9.3e-01
68 7.2e-01 7.5e-01 ... 1.2e-04 6.2e-02
69 8.6e-01 8.0e-01 ... 9.2e-01 3.4e-01
[70 rows x 10 columns]
Dataframe indexing#
All the regular pandas methods (df['mycol'], df.mycol, df.loc, df.iloc, etc.) work exactly the same. But Sciris gives additional options for indexing. Specifically, getitem commands (what happens under the hood when you call df[thing]) will first try the standard pandas getitem, but then fall back to iloc if that fails. For example:
[14]:
df = sc.dataframe(
x = [1, 2, 3],
values = [45, 23, 37],
valid = [1, 0, 1]
)
sc.heading('Regular pandas indexing')
print(df['values',1])
sc.heading('Pandas-like iloc indexing')
print(df.iloc[1])
sc.heading('Automatic iloc indexing')
print(df[1]) # Would be a KeyError in regular pandas
———————————————————————
Regular pandas indexing
———————————————————————
23
—————————————————————————
Pandas-like iloc indexing
—————————————————————————
x 2
values 23
valid 0
Name: 1, dtype: int64
———————————————————————
Automatic iloc indexing
———————————————————————
x 2
values 23
valid 0
Name: 1, dtype: int64
Dataframe manipulation#
One quirk of pandas dataframes is that almost every operation creates a copy rather than modifies the original dataframe in-place (leading to the infamous SettingWithCopyWarning.) This is extremely helpful, and yet, sometimes you do want to modify a dataframe in place. For example, to append a row:
[15]:
# Create the dataframe
df = sc.dataframe(
x = ['a','b','c'],
y = [1, 2, 3],
z = [1, 0, 1],
)
# Define the new row
newrow = ['d', 4, 0]
# Append it in-place
df.appendrow(newrow)
# Show the result
print(df)
x y z
0 a 1 1
1 b 2 0
2 c 3 1
3 d 4 0
That was easy! For reference, here’s the pandas equivalent (since append was deprecated):
[16]:
# Convert to a vanilla dataframe
pdf = df.to_pandas()
# Define the new row
newrow = ['e', 5, 1]
# Append it
pdf = pd.concat([pdf, pd.DataFrame([newrow], columns=pdf.columns)])
That’s rather a pain to type, and if you mess up (e.g. type newrow instead of [newrow]), in some cases it won’t even fail, just give you the wrong result! Crikey.
Just like how sc.cat() will take anything vaguely arrayish and turn it into an actual array, sc.dataframe.cat() will do the same thing:
[17]:
df = sc.dataframe.cat(
sc.dataframe(x=['a','b'], y=[1,2]), # Actual dataframe
dict(x=['c','d'], y=[3,4]), # Dict of data
[['e',5], ['f', 6]], # Or just the data!
)
print(df)
x y
0 a 1
1 b 2
2 c d
3 3 4
4 e 5
5 f 6
